Temporal Difference Learning

type

status

date

slug

summary

Introduction

Taxonomy of RL algorithms

The figure below provides a general, though not all-encompassing, classification of deep RL algorithm designs.

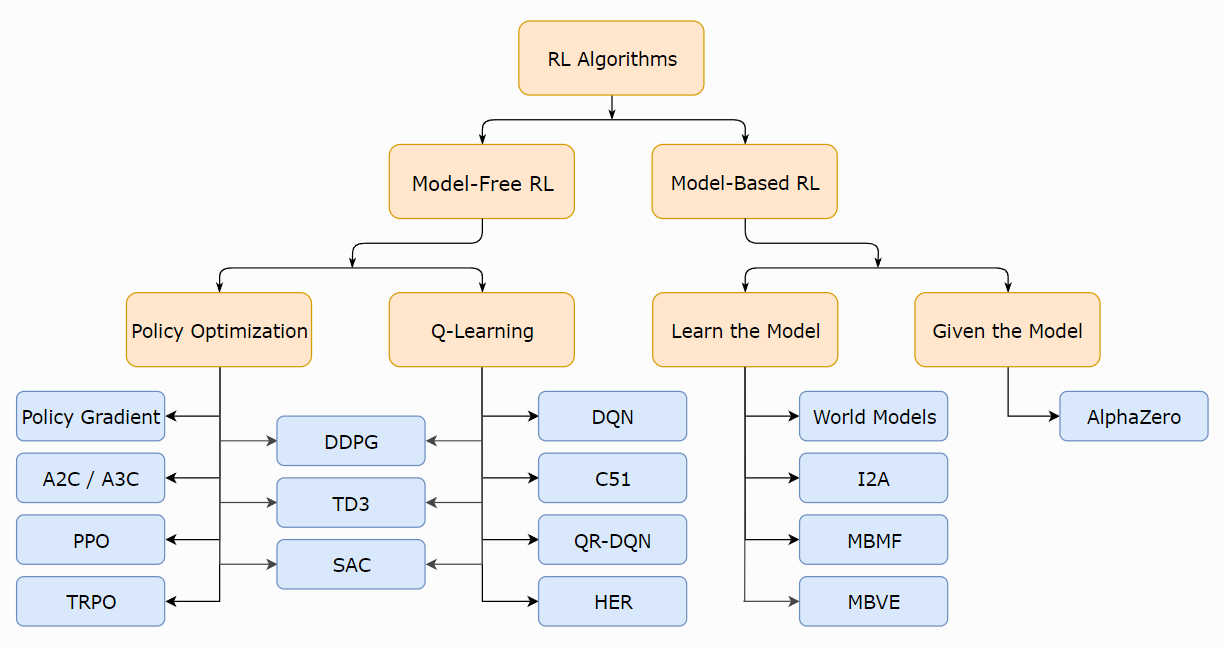
The Monte-Carlo and Temporal-Difference algorithms we will introduce in this article are both typical model-free approaches.

Monte-Carlo Algorithm

For episode , the return is defined as the total discounted reward: Our objective is to learn the value function, which is the expected return

Monte-Carlo approaches with the empirical mean sampled episode returns.

To evaluate state , we maintain the arrays and :

The first/every time-step that state is visited in an episode,

increment counter

Increment total return

Value is estimated by mean return

By law of large numbers, as

This process can also be done incrementally:

For each state with return

Often it could be useful to replace with for non-stationary problems.

TD Algorithm

Instead of the actual return , Update value toward (biased) estimated return:

is called the target

is called the error

is not dependent on the final outcome.

Dynamic Programming Backup

prioritizes exploration in stead of exploitation.

Certainty Equivalence

for the observed episodes:

converges to solution of the that best fits the data.

Its estimators are:

exploits Markov property, and are usually more efficient in Markov environments.

Bootstrapping and Sampling

ㅤ	Bootstrapping	Sampling

n-Step TD

Dene the n-step return:

n-step :

TD(lambda)

Lambda return and forward view

We combine all using weight to compute the , and formulate the forward-view of accordingly:

It is worth noting that the weights decay by a factor of , and

The weighting function can be illustrated below:

ℹ️

The weights assigned to the terminal point is the sum

Eligibility Traces

To assign a state’s eligibility with respect to its outcome, we consider its frequency and recency heuristics by writing:

e.g. for episode , the eligibility traces are:

Backward view

We keep an eligibility trace for every state . For each time step, broadcast the backwards:

When , only current state is updated.

When , total update for is the same as . Therefore, is roughly equivalent to every-visit .

ℹ️

Theorem The sum of offline updates is identical for forward-view and backward-view

Error telescoping

When , sum of telescopes into ;

For general , TD errors also telescope to , :

Consider an episode where is visited once at time-step

Online and offline updates

Offline updates

Updates are accumulated within episode

but applied in batch at the end of episode

Online updates

updates are applied online at each step within episode

Forward and backward-view are slightly different

Exact online achieves perfect equivalence

here indicates equivalence in total update at end of episode.

References

[1] Spinning Up in Deep RL, OpenAI

[2] David Silver, Model-Free Control slides

[3] Berkeley cs285