Overview of Efficient Transformers

type

status

date

slug

summary

Base Model

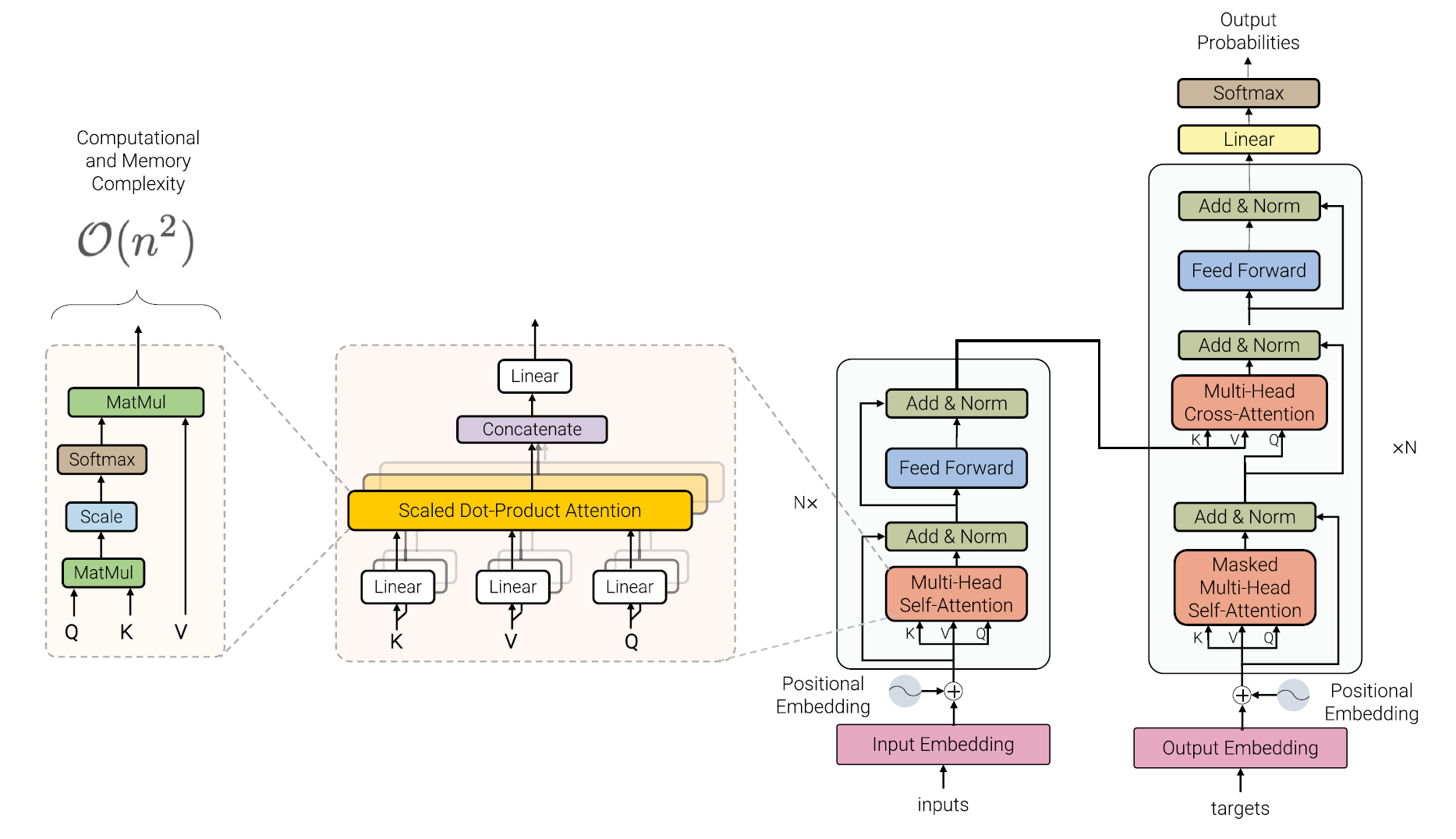
embedding [one-hot project]

+ positional encoding

Multi-Head Self-Attention

heads, , concatenate, dense. parallel:

Position-Wise FFN

for every time step, apply the same MLP to improve network expression ability (promote then reduce dimensionality).

Computation Cost

memory & cc: quadratic.

Mode

(1) encoder-only (e.g. for classification),

(2) decoder-only (e.g. for language modeling), causal, upper triangular mask

(3) encoder-decoder (e.g. for machine translation), decoder part causal due to auto-regressive

Modifications

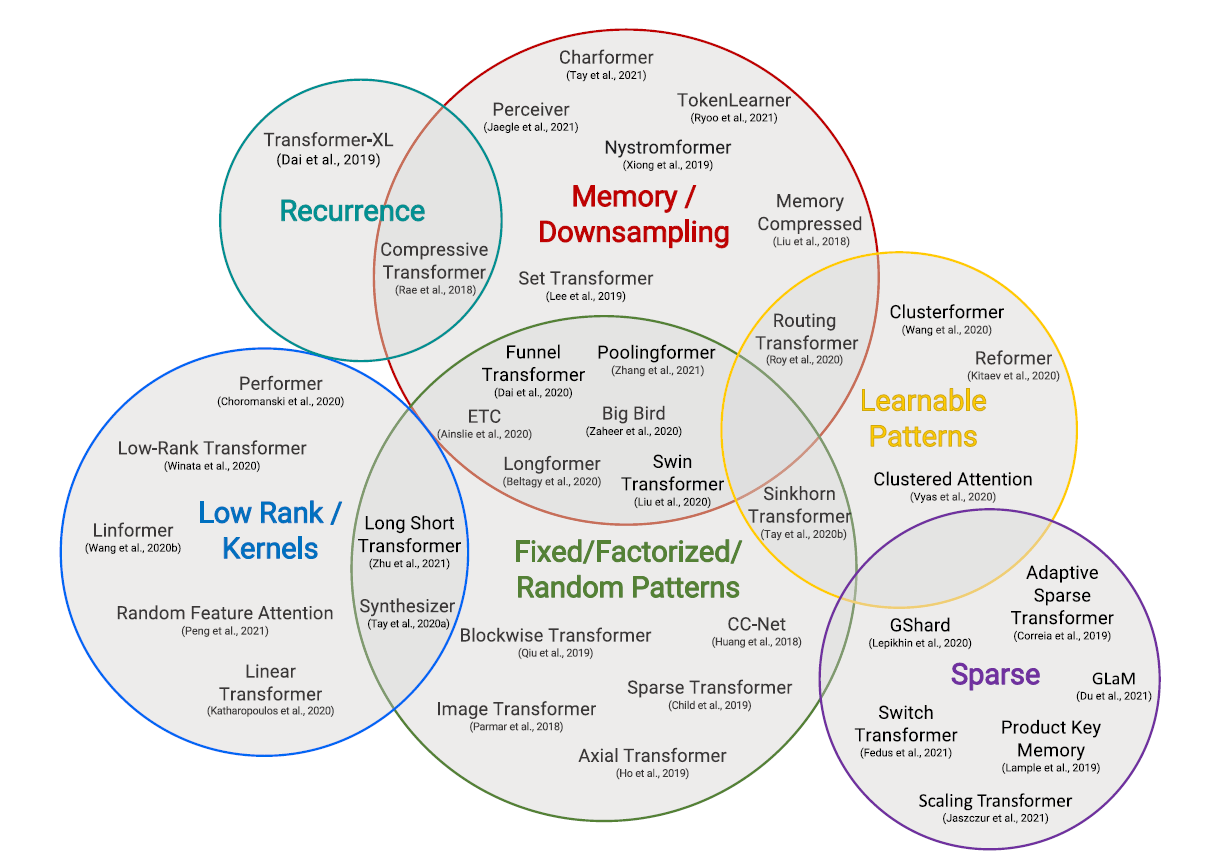
Methodology

FP (fixed patterns): local windows etc.

Block-wise Patterns:
Strided Patterns: tending by intervals. Strided or dilated windows.
Compressed Patterns: pooling, downsample sequence length.

CP (Combinations of Patterns): aggregation / combination / axial of FP

LP (Learnable Patterns): data-driven, establish token relevance -> assign to buckets/clusters

relevance: hash, k-means, sort blocks
enables global view on top of FP's efficiency

M (neural memory): learnable side memory module

Set Transformers: pooling-like compress restore information via cross attention with temporary vectors(learned)
problem: information loss global token (e.g Bert [CLS])

LR (Low rank methods): leverage low-rank approximations of the self-attention matrix

post softmax, the attention matrix is not full-rank
linformer:

where are projection layers.

KR (Kernels): re-writing of the self-attention mechanism to avoid explicitly computing the matrix

can be viewed as a form of LR

RC (recurrence): connect blocks via recurrence

DS (downsampling): e.g. patch merging in Swin-Transformer

Sparse Models and Conditional Computation: sparsely activate a subset of the parameters to improve FLOPS

Detailed Walk-Through

Image Transformer

local attention

Self-attention computed within blocks independently. for block of length ,

Memory-Compressed Attention

For , apply convolution along axis 0 with kernel size and stride to reduce dimension to . CC of attention then becomes . However, it often either

does not result in significant improvement in cc due to and being similar in orders of magnitude; or

lose information during compression.

Two Attention Schemes

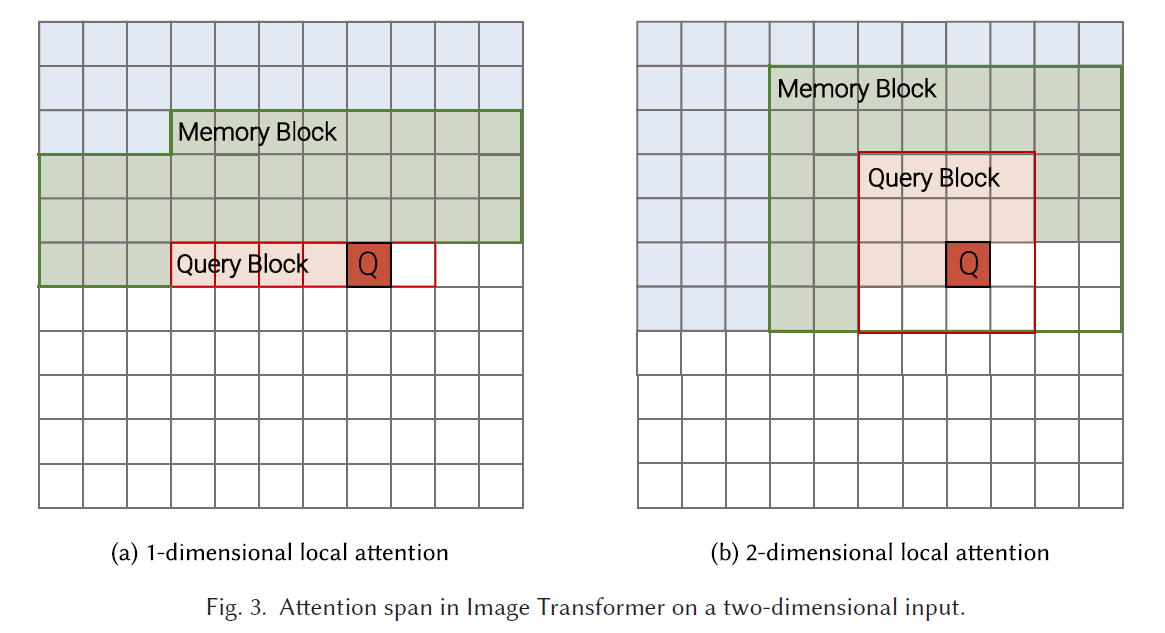
flattened in raster order, partition into non-overlapping query blocks of length , extends to memory blocks. Loses global receptive field.

Sparse Transformer

Assumption: In softmax Attention, effective weights are sparsely distributed.

heads

fixed: strided: which can be visualized below:

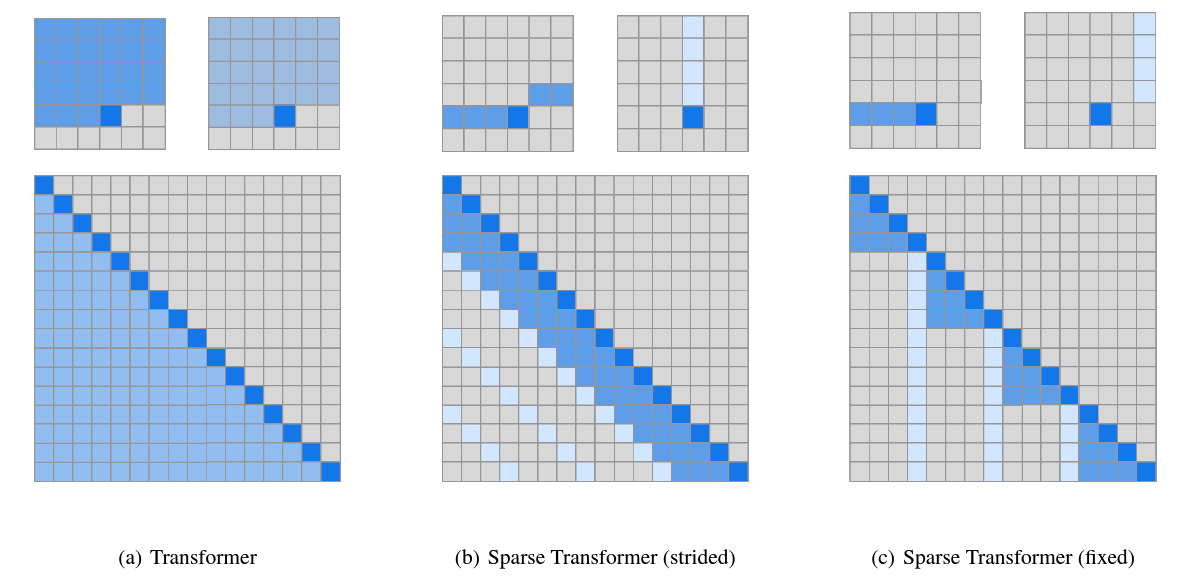
usage

alternate and : Justification: synthesizes block information, so striding in does not affect the receptive field.

merge:

multi-head, then concatenate:

cc

set , then strided attention is more suited for images and audio; (more local) fixed attention is more suited for texts. (more global)

Axial Transformer

Compute attention along axis. For image data, saves Generally, for , Axial transformer saves

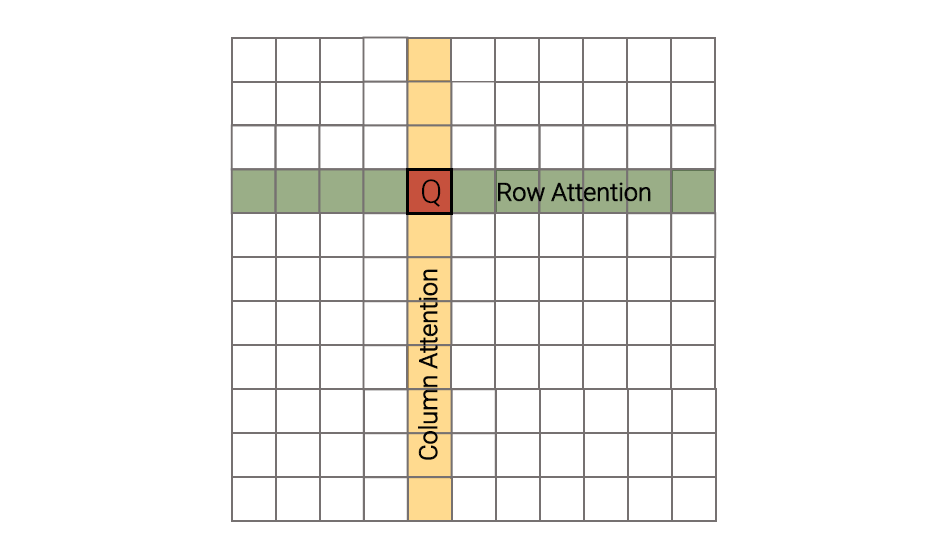
models

auto-regressive: Inner decode: row-wise model

where is the initial dimensional embedding of size shiftright ensures the current pixel is out of receptive field. Outer Decoder: capturing the rows above

The tensor represents context captured above the current pixel. Finally, pass through LayerNorm and dense layer to produce logits Effective for point clouds, etc.

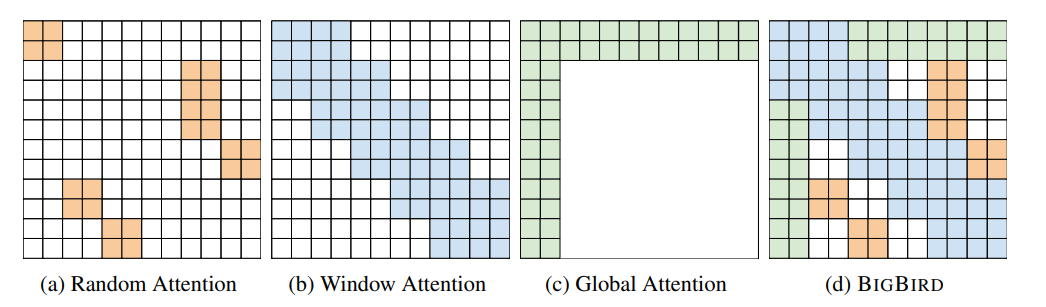
Longformer

dilated CNNs dilated sliding windows Increases the receptive field by layer like CNN, and therefore this indirect approach performs similarly bad at long distance modeling. special tokens for global attention (BERT [CLS]) , which needs to attend to and be attended by all tokens. Crucial.

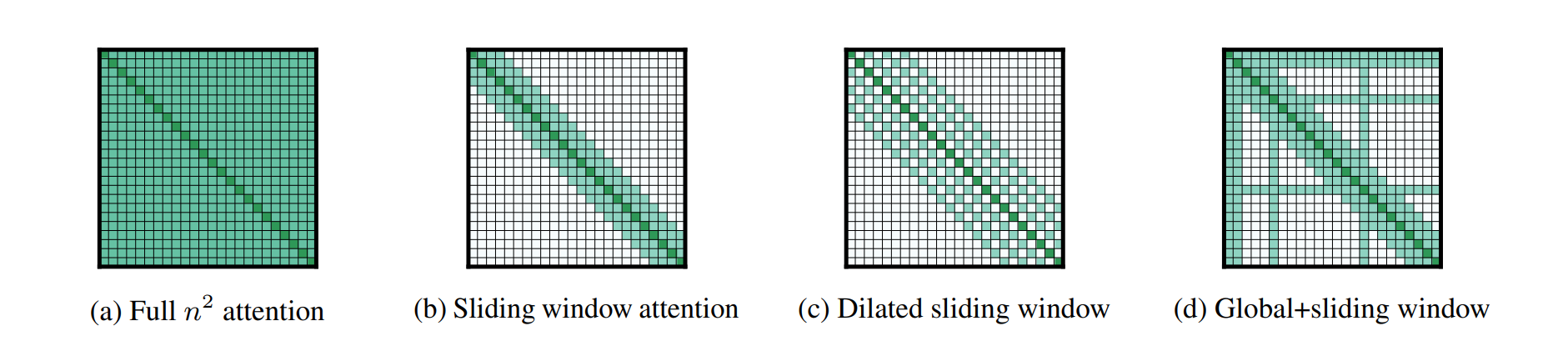
Big Bird

global tokens + fixed patterns (local sliding windows)+ random attention (queries attend to random keys). Justification for randomness: The standard Transformer is a complete digraph, which can be approximated with random graphs. The model is Turing-complete.

Routing Transformer

learns attention sparsity with k-means clustering where Cluster centroid vectors are shared for and

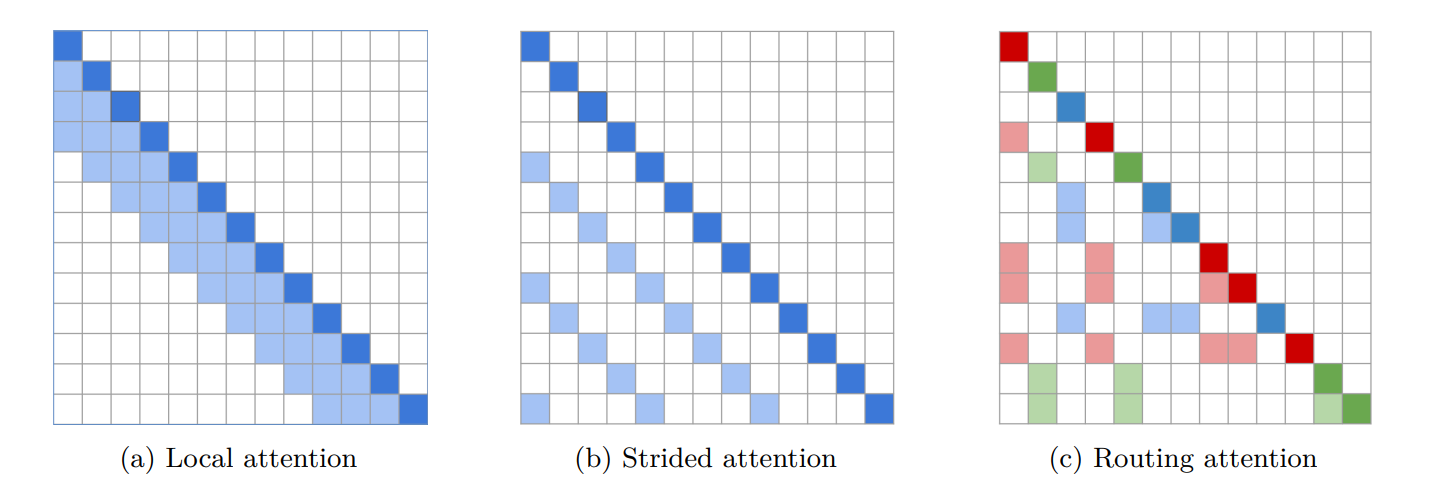
For decoder (causal attention), solutions include:

additional lower-triangular masking;

share queries and keys. Namely, Works better.

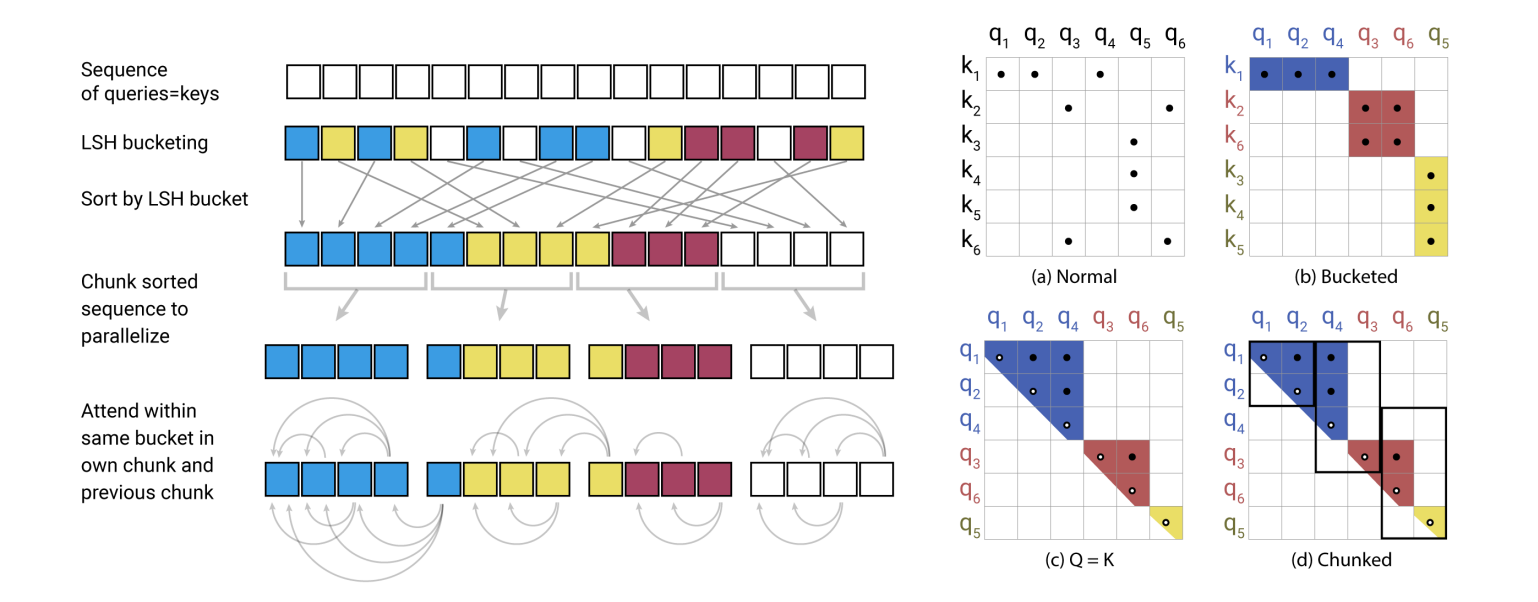
Reformer

Locality Sensitive Hashing (LSH). For hashes, define random matrix similarity with random vectors.

LSH attention:

where is the normalizing term in softmax. To avoid queries with no keys, set s.t. Multi-round:

Revnet:

Reduce memory (activation) cost with extra computation.

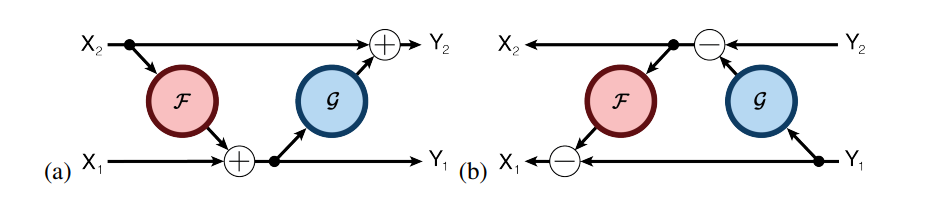
In reformer, set to LSH attention blocks, and to FFN.

Linformer

, reduction on dimension instead of Needs to maintain causal masking.

where are projections. Reminiscent of depth-wise convolutions/ pooling.

Performer

Fast Attention via Orthogonal Random Features (FAVOR): With Kernel , where is a random feature map, we can write attention as , then

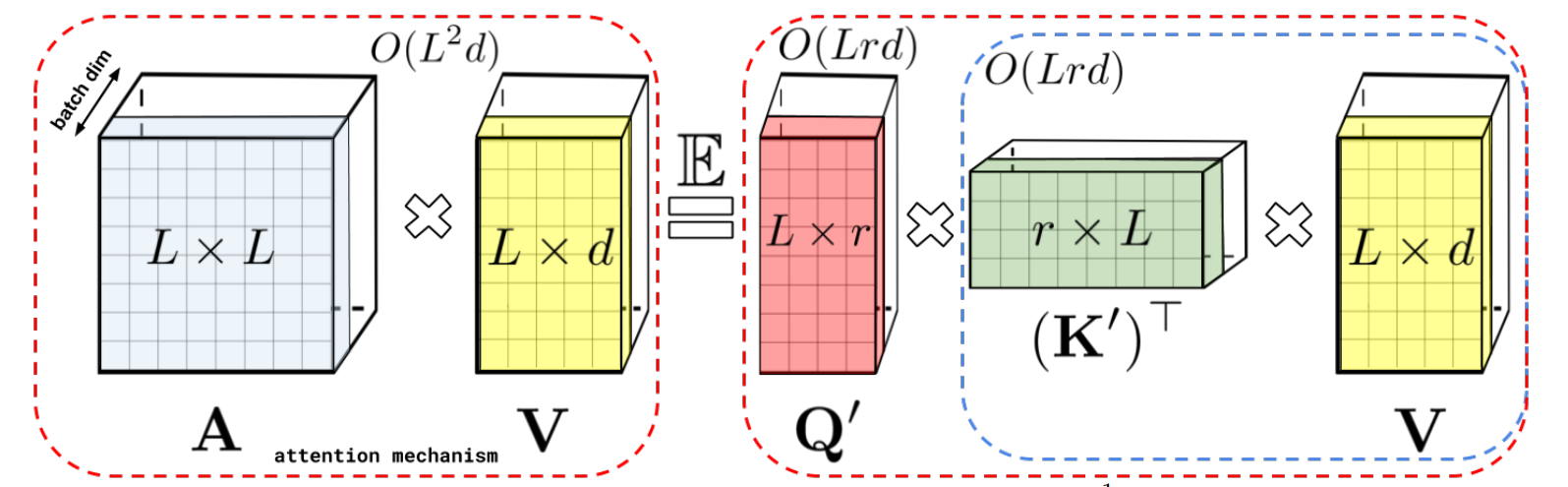
slower on causal(autoregressive) due to additional steps for masking, therefore unable to be parallelized.

Linear Transformer

kernel method, linear-time, constant memory RNN. , observe:

with kernel method: then

For unmasked, attends to the same keys, therefore we simply reuse for masked, incremental:

If to compute then cc is choose: , then

References

[1] Yi Tay, Mostafa Dehghani, Dara Bahri, and Donald Metzler. 2022. Efficient Transformers: A Survey. ACM Comput. Surv. 55, 6, Article 109 (December 2022), 28 pages. https://doi.org/10.1145/3530811