Computational efficiency of Swin-transformer

type

status

date

slug

summary

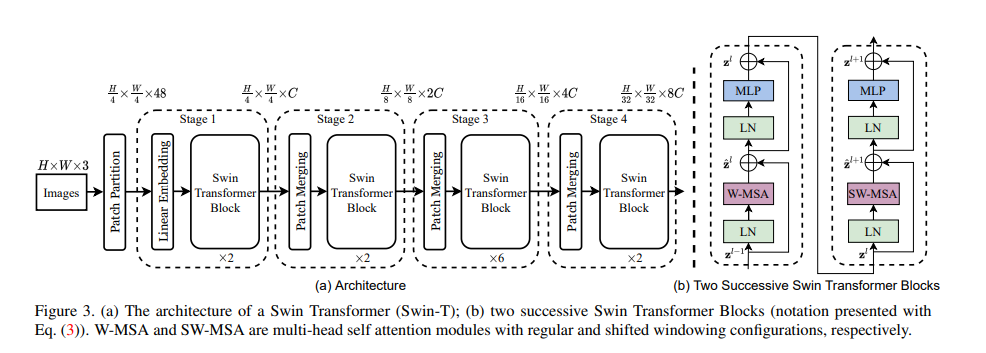
Overall Structure

The overall structure of Swin is illustrated below.

Patch merging

At stage Swin performs patch merging to downsample from to to produce a hierarchical representation.

The W-MSA module

Matrix multiplication:

could be implemented as follows:

Therefore its computational complexity is

For a global Multi-head Self Attention (MSA) module,

We can divide its computation into the following 4 steps and calculate their respective cc:

for input , compute

In total,

Let thus for the local windows,

With sufficiently small , we consider the computational complexity of Swin-transformer linear with respect to the image size .

SW-MSA

To increase modeling power by introducing connections across windows, the authors proposed a shifted window partitioning approach by displacing the windows by pixels in the sucessive layer.

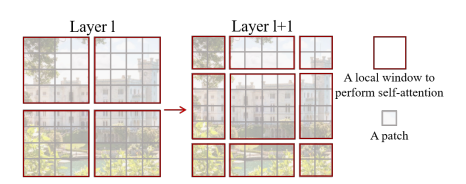
However, the number of windows is increased from to of varying sizes, hindering synchronous calculation. Therefore the proposed approach is to perform a cyclic shift and mask the correlated self-attention results in each window by to set the values near after passing through softmax.

Suppose , e.g. each local window covers patches, the four Attention Masks are visualized below:

Relative Position Bias

where parameter matrix is the rel.bias.

Define a 2D relative position index , it is clear that . We perform a simple linear transformation and use as the 1D relative position index. For each patch, we obtain a matrix of size . We flatten them individually and concatenate over patches, resulting in a matrix.

We train a vector table of length , which is the range of possible indices, to project the index values to index bias.